768. 最多能完成排序的块 II
题目描述
这个问题和“最多能完成排序的块”相似,但给定数组中的元素可以重复,输入数组最大长度为2000,其中的元素最大为10**8。
arr是一个可能包含重复元素的整数数组,我们将这个数组分割成几个“块”,并将这些块分别进行排序。之后再连接起来,使得连接的结果和按升序排序后的原数组相同。
我们最多能将数组分成多少块?
示例 1:
输入: arr = [5,4,3,2,1]
输出: 1
解释:
将数组分成2块或者更多块,都无法得到所需的结果。
例如,分成 [5, 4], [3, 2, 1] 的结果是 [4, 5, 1, 2, 3],这不是有序的数组。
示例 2:
输入: arr = [2,1,3,4,4]
输出: 4
解释:
我们可以把它分成两块,例如 [2, 1], [3, 4, 4]。
然而,分成 [2, 1], [3], [4], [4] 可以得到最多的块数。
注意:
arr的长度在[1, 2000]之间。
arr[i]的大小在[0, 10**8]之间。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/max-chunks-to-make-sorted-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。方法 1: 滑动窗口
思路
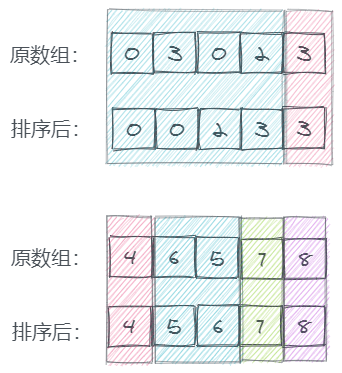
复杂度分析
代码 (JS/C++)
方法 2: 单调栈
思路
图解
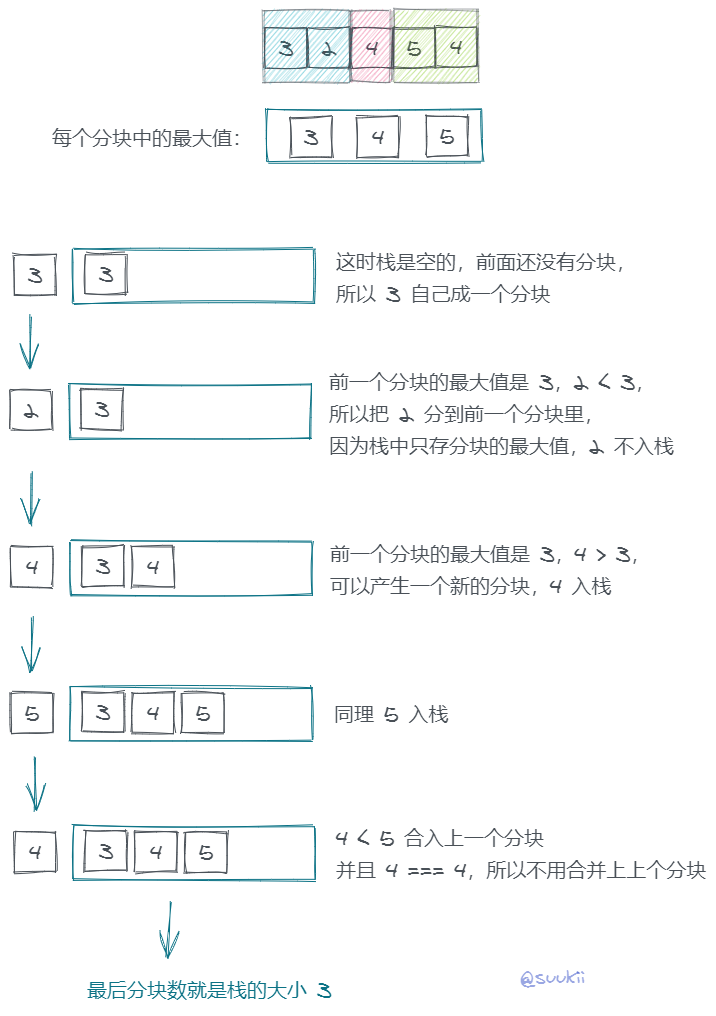

复杂度分析
代码(JS/C++)
Last updated