Big O 算法复杂度

bigocheatsheet

循环 - 时间复杂度

Code	Complexity
	O(n) for 循环执行了 n 次
	O(n^2) 外层 for 循环执行了 n 次， 每一次循环，内层的 for 循环也执行了 n 次， 一共执行了 n^2 次
	O(n^3) 外层 for 循环执行了 n 次， 每一次循环，内层的 for 循环执行了 n^2 次， 一共执行了 n^3 次

高斯求和 - 时间复杂度

如果在一个算法中，一段代码先执行了 1 次，然后执行 2 次，...，执行 N 次，那这个算法的时间复杂度就是：

1 + 2 + ... + N

用高斯求和法来求这个式子的结果，我们可以得到：

(n * (n + 1)) / 2

也就是：

1/2 * n^2 + 1/2 * n

忽略掉常数，结果就是 n^2。

二分查找 - 时间复杂度

二分查找就是每次都将问题的规模减半，直到我们找到目标元素。在最坏的情况下，我们要把规模减少到只剩 1 个元素才能找到目标。那要求二分查找的时间复杂度，就变成了要求：

经过多少次操作才能把 n 变成 1

这个问题的答案。假设经过 x 次操作后 n 变成了 1，那么：

n / 2^x = 1

所以：

x = log2n

我们一般会把底数忽略掉，所以最终的复杂度就是 O(logn)。

递归 - 时间&空间复杂度

时间复杂度

最简单的情况下，只需求递归函数一共被调用了多少次就好了，也就是递归树最多有多少个节点。

一个简单的公式是：O(b^d)

• b 是递归树的最大分支数，也就是在一个函数中，最多调用了多少次递归函数。

• d 是递归树的最大深度。

以 Fibonacci 的递归函数为例：

function fib(n) {
    if (n <= 1) return 1;
    return fib(n - 1) + fib(n - 2);
}

它的递归树是这样的：

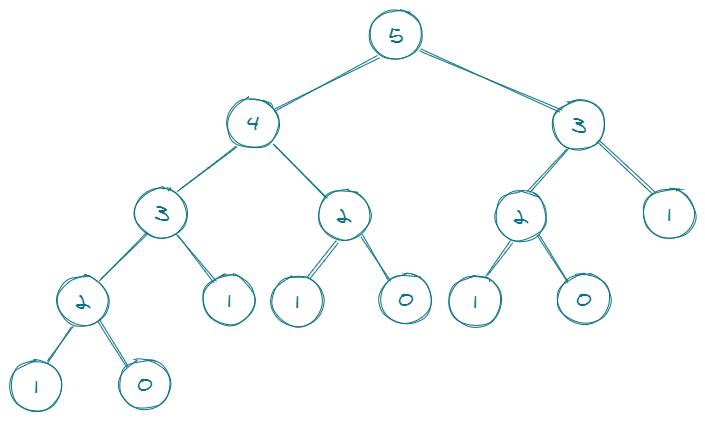
• 在每个 fib 函数中，fib 都被调用了两次，所以递归树的最大分支数是 2

• 递归树的最大深度是 n

如果把这棵树填满的话，那它会有

2^0 + 2^1 + 2^2 + ... + 2^(n-1)

个节点，也就是 2^n 个节点。所以，fib 递归函数的时间复杂度是 O(2^n)。

空间复杂度

只需要数一下到达递归出口 if (n <= 1) return 1 前，一路调用了多少次递归函数。

也就是，从递归树的顶点出发，选择一条路径一路往下，到达最底下的那个叶子节点(递归出口)，一路上经过了多少个节点。

一般来说，递归算法的空间复杂度是 O(h)，h 是递归树的最大深度。

上述 fib 函数的空间复杂度就是 O(n)，n 刚好是递归树的最大深度。

此处讨论的只是调用栈的空间复杂度