32.最长有效括号

https://leetcode-cn.com/problems/longest-valid-parentheses/

题目描述

给定一个只包含 '(' 和 ')' 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"
示例 2:

输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-valid-parentheses
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

方法 1：滑动窗口

思路

  1. 首先最短的有效括号字符串就是一对括号 ()，那我们可以先在字符串 s 中找到这样一对括号。

  2. 然后，把这对括号作为一个滑动窗口的中心，分别向左右两侧扩大滑动窗口，窗口内是有效括号。

  3. 当滑动窗口不能再扩大时，把当前窗口的左右边界记录下来，然后，从这个窗口的右边界开始，重复步骤 1 到 3，直到字符串遍历结束。

  4. 等等，还漏了一种情况。当我们在扩大滑动窗口的时候，如果碰到了另一个窗口的边界，那这两个窗口加起来也是一个有效括号字符串。所以，我们得把这两个窗口作为新的滑动窗口中心，然后向两侧扩大窗口。

  5. 因为我们是从左往右遍历字符串，所以窗口相碰的情况只有一种，就是当前窗口的左边界碰到了前一个窗口的右边界，我们只要判断这种情况就行。

图解

代码

JavaScript Code

/**
 * @param {string} s
 * @return {number}
 */
var longestValidParentheses = function (s) {
    const expand = (s, l, r) => {
        while (s[l - 1] === '(' && s[r + 1] === ')') {
            l--;
            r++;
        }
        return [l, r];
    };

    const map = {};

    let l = 0,
        r = 0,
        max = 0;
    while (true) {
        // 以括号对为中心
        l = s.indexOf('()', r);
        if (l === -1) break;

        r = l + 1;
        // 向左右两边不断扩大滑动窗口
        [l, r] = expand(s, l, r);

        // 当窗口扩大到最大时，
        // 如果当前窗口的左边界刚好挨着前一个窗口的右边界，那么，
        // 合并这两个窗口，再以这个新合并的窗口为中心，向两侧扩大滑动窗口
        while (l - 1 in map) {
            [l, r] = expand(s, map[l - 1], r);
        }
        // 记录当前窗口的左右边界，key 是窗口右边界，value 是窗口左边界
        map[r] = l;
        // 更新最大窗口
        max = Math.max(max, r - l + 1);
    }

    return max;
};

复杂度分析

  • 时间复杂度：$O(n)$，n 为字符串的长度。

  • 空间复杂度：$O(n)$，n 为字符串的长度。

方法 2：动态规划

思路

我们可以用一个一维数组 dp 来记录 以当前坐标为结尾的有效括号字符串的长度是多少 这个状态。

关键是，怎么找到当前坐标的状态 dp[i] 跟 i 之前坐标的状态的依赖关系。

  • 如果当前坐标 i 是一个左括号 '('，很明显有效字符串不会以左括号为结尾，所以这个状态是 0；

  • 如果当前坐标 i 是一个右括号 ')'，那么：

    • 如果它前一个 i - 1 是 '('，它们可以组成一对儿，那么 dp[i] 至少是 2

    • 如果它前一个 i - 1 是 ')'，虽然它们不能成对儿，但是，')' 说明它可能是某个有效字符串的结尾，那我们就得检查这个坐标 i - 1 的状态了：

      • 如果 dp[i-1] 是 0，那就没戏了，dp[i] 也只能是 0 了

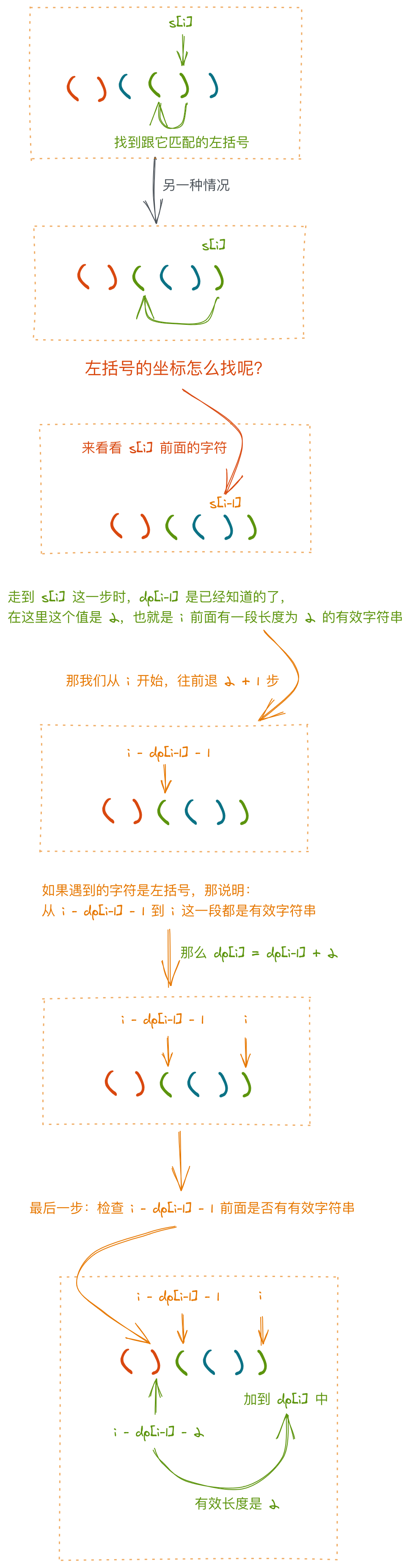
      • 如果 dp[i-1] > 0，那么，i 的前面有一段有效括号字符串，那只要判断这段字符串前面的那个字符是不是 ( 就好了，如果是，dp[i] = dp[i-1] + 2，如果不是，dp[i] = 0

    • 等等，还没有结束，如果到了这里，dp[i] 大于 0 的话，还有一种情况，跟滑动窗口解法里面的一样，它的左边可能还有一段紧挨着的有效括号字符串，所以我们得把这段字符串的长度也加到 dp[i] 中。

图解

代码

JavaScript Code

/**
 * @param {string} s
 * @return {number}
 */
var longestValidParentheses = function (s) {
    // 状态：以当前字符结尾的字符串，最长的有效括号长度是多大
    const dp = Array(s.length).fill(0);

    for (let i = 1; i < s.length; i++) {
        // 有效括号只能是以 ')' 结尾的
        // 所以，以 '(' 结尾的字符串，最长有效括号长度就是 0，不用管
        if (s[i] === ')') {
            // 遇到 ')' 时，往左边去找跟它匹配的 '('，如果存在，那么有效长度在 dp[i - 1] 基础上加 2

            // dp[i - 1] 是以 s[i - 1] 结尾的字符串的最长有效括号长度，设它为 k，
            // 也就是 [i - k, i - 1] 这段是有效括号字符串，
            // 如果这段字符串前面的那个字符 s[i - k - 1] 是 '(' 的话，那么有效长度加 2
            if (i - dp[i - 1] - 1 >= 0 && s[i - dp[i - 1] - 1] === '(') {
                dp[i] = dp[i - 1] + 2;

                // 如果匹配到的 '(' 前面还有有效长度的话，也加上
                if (i - dp[i - 1] - 2 > 0) {
                    dp[i] += dp[i - dp[i - 1] - 2];
                }
            }
        }
    }
    return Math.max(...dp, 0);
};

复杂度分析

  • 时间复杂度：$O(n)$，n 为字符串的长度。

  • 空间复杂度：$O(n)$，n 为字符串的长度。

方法 3：栈

思路

用一个栈来检查括号的有效性，用一个数组 valid 来记录匹配括号对的位置。

  • 栈的用法跟20.有效括号里的一样，不过入栈的不是 (，而是它们的下标。

  • 在遍历过程中，如果碰到 )，就从栈中弹出一个元素，这个元素就是 ) 对应的 ( 的下标。

  • 接着我们在 valid 中这两个下标对应的位置做个标识 1，说明这里找到了一对有效括号。

  • 等遍历结束之后，在 valid 中找到连续最长的 1 序列。

代码

JavaScript Code

/**
 * @param {string} s
 * @return {number}
 */
var longestValidParentheses = function (s) {
    const valid = Array(s.length).fill(0);
    const stack = [];

    for (let i = 0; i < s.length; i++) {
        if (s[i] === '(') stack.push(i);

        if (s[i] === ')' && stack.length > 0) {
            // Mark the open and close indices as 1 in valid.
            valid[i] = 1;
            valid[stack.pop()] = 1;
        }
    }

    // Find longest sequence of 1s.
    let count = 0,
        max = 0;
    for (let v of valid) {
        v && count++;
        v || (count = 0);
        count > max && (max = count);
    }
    return max;
};

复杂度分析

  • 时间复杂度：$O(n)$，n 为字符串的长度。

  • 空间复杂度：$O(n)$，n 为字符串的长度。

Previous62.不同路径Next20.有效括号

Last updated

Was this helpful?